LondonIndicators
(This graph should update three times daily, once for each curve. The last few values may be subject to some retrospective change as a consequence of the estimation and smoothing algorithms that use future values.)
Description
Note/update: my description below of the green line, which was meant to be based purely on Zoe symptom data, is not correct. (Thanks to Alan Jenkins for pointing this out.) Effectively what it calculates is Zoe's incidence measure (though a slightly leading version of it), which is based on both testing and symptom data and is still useful. Over the next few days I will try to either change this curve to what I originally wanted it to be, or to rewrite its description to be more accurate.
The purpose of this page is to try to help see how containable the new variant (B.1.1.7 lineage) is. The idea is to take London, a large population which has been affected early and for which the new variant is now dominant, and look at two indicators derived from the Covid Symptom Study run by Zoe, and accompanying swab/PCR tests (known here as "Zoe" for short) in order to get an early idea as possible as to whether the stringent containment measures imposed on 20 December 2020 are enough to prevent growth in infections. This question has a bearing on how bad things are likely to get nationally and worldwide.
The most reliable indicators of virus prevalence are random sample swab/PCR test surveys, and these are carried out for the ONS and for Imperial College London as part of the REACT surveys. Unfortunately there is a long lead time on results from these and I'm impatient to know as soon as possible whether we're going to be overrun by this variant.
By contrast, Zoe provides two streams of information which, although subject to biases in a way that a random sample survey isn't, should be faster to respond. The two streams are: (i) an indication, from people reporting their symptoms on an app, of how many people at any one time have symptomatic Covid-19 ("prevalence"), and (ii) a rolling swab/PCR-test based survey based on inviting selected app users to take a test, reporting a 14-day average of test results from 18 days before the present day to 4 days before the present day. (The symptom-based prevalence estimate is also adjusted to match known prevalence through random sampling, but I assume this is a fairly fixed or slow-varying factor, and so won't change the multiplicative trends too much.)
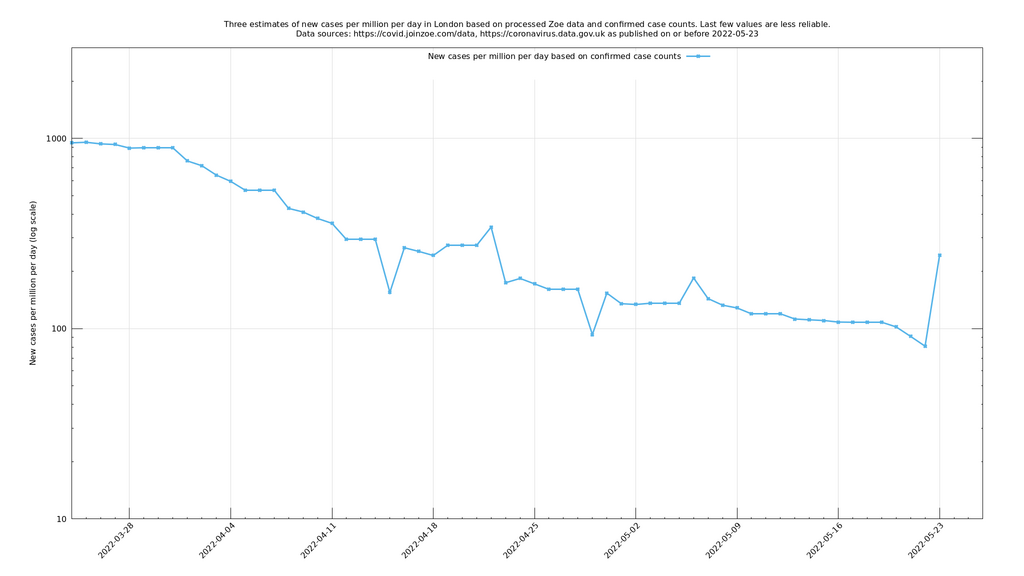
Both of these indicators, taken at face value, are influenced by new Covid-19 cases stretching back three weeks or so: they are averages over the recent past. You can attempt to undo these averages to get a more up-to-date result - an estimate of new Covid-19 cases a few days ago - and that is what the purple and green lines in the above graph represent. The blue line is the number of daily confirmed cases in London, as obtained from the official data stream and is included for reference.
You would hope that the purple and green lines are leading indicators and anticipate changes in the blue line (confirmed cases), so you might imagine the blue line shifted to the left to help it coincide with the other lines, but this is not obviously so and I am not going to try to make a definite such claim along these lines. Instead, I'll include a description in the appendix of how these lines were calculated and people can decide how much they choose to believe in them. I am provisionally regarding them as fair indicators, but not infallible.
Conclusion at 1 January 2021
At the time of writing, IF these green and purple curves are an accurate, and IF they are up-to-date enough for the last values to be mostly based on the last 12 days, then we could be in trouble because just flatlining isn't good enough. Bear in mind that roughly 20% of London has already had Covid-19, mostly from the first wave which we expect should give some degree of immunity, so we might expect the growth elsewhere in the country and world will be even more difficult to contain.
Of course the effect of Christmas muddies the waters somewhat. It's possible that the Christmas period causes more (and varied) contacts than usual, but it's also possible that it's the other way around, with schools shut, many off work, and only a minimal Christmas exemption against restrictions on personal meetings.
This simple indicator, LondonTraffic, suggests that traffic on the road has been considerably down from usual since 20 December 2020, maybe comparable to the latter part of May 2020, but higher than in April 2020 where the country was at its most locked down, and Apple mobility data says something similar. So there is perhaps some scope for tightening up, but maybe not a great deal.
Conclusion at 11 January 2021
The green (symptom-based) and purple (test-based) lines have been on a decline since around 2 January. The blue line (confirmed cases) is roughly stable or possibly declining - a little too early to say for sure. I don't really believe the purple line can drop this fast (would mean R~=0.5), and it really should not be going below confirmed cases, itself probably a significant underestimate. I don't know if there is something wrong with my treatment or something wrong with the underlying test-based data.
Not that this is a very scientific assessment or anything, but the green line looks fairly plausible by eye - it stays above confirmed cases which is good and doesn't jump too fast. If it were to anticipate a fall in confirmed cases over the next week, then that would be a little evidence that it has some predictive value. On the assumption that the green line is reliable, what would it mean? Its slope over the last week would correspond to an R of roughly 0.8. Unfortunately since writing the previous conclusion, I've learnt that 20-25% is a rather low-end estimate for the current attack rate (number of people who have been infected) in London, and other analysts estimate 25-30% or even 40%. If it is 30%, then that means that roughly 0.7 of the cutdown on R could be due to immunity, which means the current level of suppression would result in R~=0.8/0.7~=1.14 in a completely susceptible community. It's true there is more we could do to suppress the virus (schools are closed, but in fact open to quite a lot of people, places of worship still open, more jobs classified as essential compared to April, support bubbles etc), but it would obviously be quite painful to do so. So if the preceding analysis/guesswork is correct, it looks like B.1.1.7 is going to be very tough to suppress if it arrives in big numbers around the world in a couple of months, as it looks like it might.
Appendix
For the symptom/app-based data (green line), let \[I_t = \text{number of new symptomatic cases between days } t-1 \text{ and } t \text{, for }t=-k+1,\ldots,d\] \[P_t = \text{Estimated symptomatic prevalence at day }t\text{, for }t=0,\ldots,d\] \[T = \text{ recovery time random variable } \sim \Gamma(\text{shape=}2.595, \text{ scale=}4.48)\]
Here $$d$$ is the current day number, $$P_t$$ is Zoe's estimate given to us for current symptomatic prevalence, and $$I_t$$ is what we would like to deduce. The distribution of $$T$$ is taken from Varsavsky et al, December 2020 and $$k$$, the kernel size, is taken large enough to capture almost all of its tail. Given these, we seek to minimise: \[\sum_{t=0}^d \left(P_t-\sum_{i=0}^{k-1}\mathbb P(T>i+\tfrac12)I_{t-i}\right)^2 + \lambda^2\sum_{t=-k+1}^{d-1}(I_t-I_{t+1})^2\]
This is fairly crude stuff but hopefully not too far removed from reality. $$\lambda^2$$ represents the ratio of the variances of the assumed prior normal error distributions of $$P_t$$ and $$I_t$$ from their respective predictors. I would like to say that $$\lambda$$ was chosen in a principled way that maximised the predictive ability of the output, or from knowing from basic biology how much $$I_t$$ can vary from day to day, or something, but I confess I just fiddled around with it until it looked like it was producing something reasonable (neither implausibly flat nor implausibly wiggly to use technical terms) which ended up being at $$\lambda=1$$. (To be fair, varying it a bit didn't make a huge difference.)
For the swab/test data (purple line), let $$I_t$$ be the number of new symptomatic cases, as before, and let
\[S_t = \text{the published number of daily new cases on day }t\text{, for }t=0,\ldots,d\]
Then the operation is essentially the same as above, but with a two-week top hat kernel:
\[\sum_{t=0}^d \left(S_t-\frac{1}{14}\sum_{i=0}^{13}I_{t-i}\right)^2 + \rho^2\sum_{t=-13}^{d-1}(I_t-I_{t+1})^2\]
Here I chose $$\rho=0.2$$. (You'd expect $$\rho<\lambda$$ because daily new cases are lower than prevalence numbers.)