A note on the estimation of the specificity of Lateral Flow Device (LFD) tests as used in English schools up to 3 March 2021

Author: Alex Selby, 15 March 2021.

Background and Conclusion

There has been some controversy over the use of LFDs for mass screening, in particular in the case of secondary school students. One of the criticisms that has been levelled at this process is that it will generate a substantial number of false positives. What is known about the specificity appears to be an increasing series of lower bounds generated from successively lower test positivity rates in a declining epidemic. The latest simple lower bound on specificity for secondary school students is roughly 99.944% arising from the 0.056% test positivity rate. (Tests conducted, table 7, column J, taken from NHS Test and Trace weekly statistics, 11 March 2021). (Incidentally, a slightly better bound would be obtained by considering everyone who is tested at a secondary school or college, including staff, but we are concentrating on students in this note.) A more careful approach taking into account possible statistical fluctuations was carried out by Funk and Flasche and this lead to a lower bound of 99.93%, using earlier NHS Test and Trace statistics from 25 February 2021.

There is also a 99.97% specificity estimate (as opposed to lower bound) from this DHSC report, 10 March 2021.

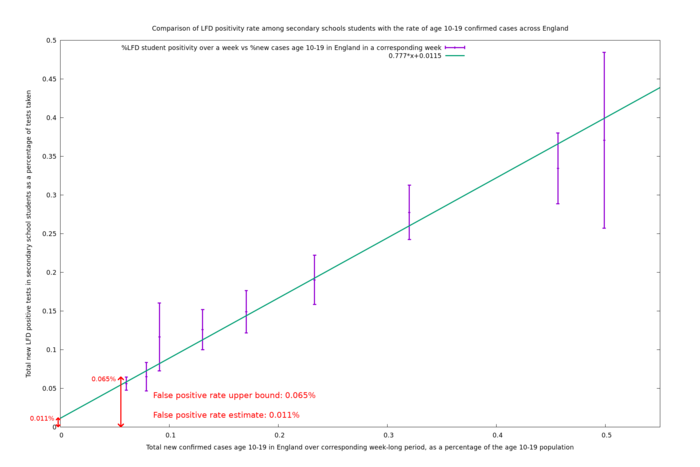
This note estimates specificity of LFD tests carried out on secondary school students to be 99.988% (99.980% - 99.995%), equivalent to a false positive rate of 0.012% (0.005% - 0.020%), based on the assumption that LFD true positives at school are proportional to the number of cases detected nationally within the student age group at a suitable date offset. (Note that the range of values given here reflects statistical uncertainty within the modelling assumptions. If the model is wrong then the true value could exceed these bounds.)

If the false positive rate is 0.012% then we can expect 79% (from 1-0.012/0.056) of the 0.056% found to be positive in the week ending 3 March to genuinely have the disease (this 79% figure is known as the positive predictive value, or PPV). In the future the PPV may decrease if disease prevalence declines, or it may increase because we are now moving from testing only asymptomatic students with LFD tests to testing all students (though see caveat below about moving from supervised to unsupervised testing).

The Idea

Imagine in one particular week 100,000 students are tested with LFDs, of which 100 come up positive. Suppose also that in that same week there are 10,000 confirmed cases nationally in the 10-19 age band. Now let's imagine in a different week 200,000 students are tested with LFDs, but only 1,000 cases are confirmed nationally. How many of these 200,000 LFD tests do we expect to come back positive?

If all 100 LFD-positives from the first week were false, then we'd expect 200 to come back positive in this new week, because with twice as many students being tested, there is twice the opportunity for false positives. On the other hand, if all 100 of the original LFD-positives were true then we'd now expect about 20 to come back positive, because although we're testing twice as many people, infection rates have come down by a factor of ten overall and 100*2/10=20.

So we see the question is whether the number of positive results from LFD tests tracks (a) the number of LFD tests carried out, or (b) (number of LFD tests carried out)*(rate of infection in the country), or somewhere in between. (a) would indicate false positives, and (b) true positives. Or to put it another way, is the LFD positive rate (positive results per test) a constant, or is it proportional to the national prevalence of the disease, or somewhere in between?

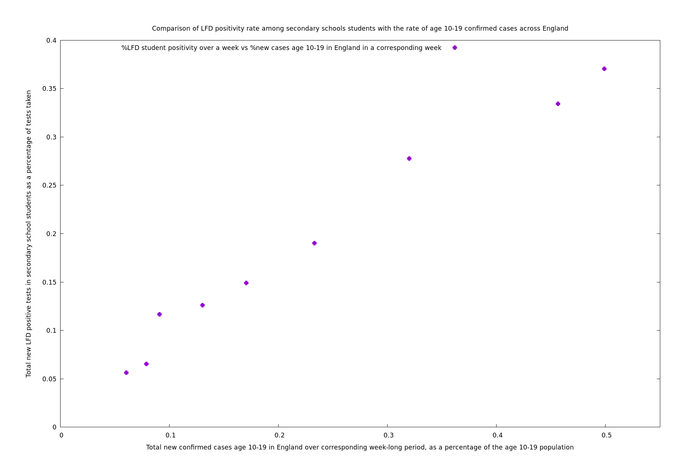
It's actually easy to determine this because we have nine weeks of data (at the time of writing). We can plot the test positivity rate against national prevalence and see if the graph looks like a flat horizontal line, or more like a sloping line that goes through the origin, or just a random mess. As we see in the figure below, it is quite close to a line that goes through the origin. In such a picture, the y-intercept (how much the line misses the origin) is our prediction of the false positive rate.

Method

The lower bounds for specificity are based on the fact that there can't be more false positives than actual positives. However, it is unlikely that all of the positives are false. In particular, we can see from Fig. 1 below that over past weeks that the school LFD positivity rate is strongly correlated with the number of confirmed cases nationally in the age band 10-19. (The third dot that is apparently a little off the best fit line corresponds to the week of half term, ending 2021-02-17, where only 27 positive results were returned, so the vertical error bar for this point is large as can be seen from Fig. 2 further below, and possibly that week is of a different nature to the others. However, it makes little difference to the overall results whether or not this data point is included in the analysis.)

Fig. 1 (click to enlarge)

It seems reasonable to suppose that the proportion of positive school LFD tests is a constant (the false positive rate) plus a term proportional to the national positivity rate for a suitably offset time period. In this picture, the false positive rate is the $$y$$-intercept of the best fit line through these points. In symbols, we assume the model

\[ m_i \sim \operatorname{Po}((\alpha +\beta q_i)n_i), \]

where $$\operatorname{Po}$$ is the Poisson distribution, $$m_i$$ is the number of LFD positives, $$q_i$$ is the rate of confirmed cases nationally (number of cases divided by age band population), $$n_i$$ is number of LFD tests carried out, and $$i$$ indexes the week. (Test and Trace statistics are given as weekly aggregates, so we work with that.) The variables are $$\alpha$$ (the false positive rate), $$\beta$$ (the relative rate at which cases are picked up by this LFD screening programme compared to nationally), and a third variable representing the day offset which determines exactly which week of national cases corresponds to the week of LFD tests. To estimate $$\alpha$$, $$\beta$$ and the offset, we maximise the log likelihood, which is $$\sum_i[ m_i\log((\alpha +\beta q_i)n_i)-(\alpha +\beta q_i)n_i]$$, up to a constant. To estimate the uncertainty in $$\alpha$$ we use $$1.96J(\alpha,\beta)^{-1/2}$$, where $$J(\alpha,\beta)=\sum_i m_i/(\alpha +\beta q_i)^2$$ is the observed Fisher information of $$\alpha$$, the negative of the second derivative of the log likelihood with respect to $$\alpha$$. The $$1.96$$ arises in the usual way as the number of standard deviations of a normal distribution that gives a 95% confidence interval.

Program and data to reproduce the results shown here can be found in this github repository: https://github.com/alex1770/Covid-19/tree/LFDwriteup.2021-03-15/LFDevaluation.

A negative binomial distribution with a common dispersion parameter was also tried instead of a plain old Poisson distribution (thanks to David Spiegelhalter for this suggestion), but it was found this made very little difference to the result. Perhaps this not so surprising because the datapoints line up so nicely that any vaguely sensible form of regression is likely to lead to a similar best fit line.

Results

Fig. 2 (click to enlarge)

The result of the maximum likelihood estimation is that $$\alpha=0.000115$$, $$\beta=0.777$$, which means the central false positive rate estimate in this situation is 0.011% (0.005% - 0.018%). The best offset turned out to be -3 days, meaning LFD tests conducted in the week ending 2021-03-03 are related to national case numbers (by specimen date) in the week ending 2021-02-28.

This -3 day offset was not quite as expected since it implies the national cases (by specimen date) are anticipating the school LFD results by 3 days. I would have expected something more like a +2 day offset arising as the difference between delays from the date of infection in the two situations: (Situation 1) there is a delay of around 3.5 days until you become LFD-positive, then a further delay of around 1.75 delays on average while you wait until your twice-weekly test comes around, making a total delay of around 5.25 days. (Situation 2) there is a delay of around 5 days until you become symptomatic, followed by some period of time, guessed to be around 2 days, for you to make up your mind to take a test and actually procure it, making a total of maybe 7 days.

However, offsets from -8 to +1 have similar likelihoods so there isn't much to choose between them. I would suppose (not investigated thoroughly) the indifference between these options might be due to the fact that cases have been declining with something like exponential decay, which could make small offsets nearly equivalent (just inducing a change in $$\beta$$). Large offsets really are different because the curve of infections doesn't look self-similar enough if you displace it from itself by too much. It is still comforting that more extreme offsets definitely fare a lot worse, since if the correlation between LFD-positives and national cases had been a complete fluke, there would have been no reason to expect it to work better at offset 0 than offset +/-20.

There is a possible mechanism by which the correlation between LFD positivity in schools and national confirmed cases could be bogus: the correlation could simply arise from schools' LFD positives being fed directly into the national confirmed cases (which are a composite of LFD-positives and PCR-positives). In fact the number of LFD positives arising from secondary school students is much smaller than the national number of confirmed cases for the 10-19 age band, so this isn't likely to be a major bias, but to check that this was not a significant problem, the program was rerun with the national confirmed cases diminished by the number of LFD-positives arising from schools. This change lead to similar results: a false positive rate estimate of 0.013% (0.007% - 0.020%). To be conservative, we take the union of this range with the original one, and (slightly arbitrarily, though it makes little difference) average the two central estimates to get a final estimate of 0.012% (0.005% - 0.020%).

Program output (using unmodified national confirmed cases):

Using LFD school numbers from table 6 of https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/968462/tests_conducted_2021_03_11.ods
Using England cases by age from https://api.coronavirus.data.gov.uk/v2/data?areaType=nation&areaName=England&metric=maleCases&metric=femaleCases&format=csv

Offset -15. Log likelihood = -52.4414
Offset -14. Log likelihood = -45.0543
Offset -13. Log likelihood = -41.0264
Offset -12. Log likelihood = -41.5126
Offset -11. Log likelihood = -37.3588
Offset -10. Log likelihood = -34.8682
Offset  -9. Log likelihood = -35.0374
Offset  -8. Log likelihood = -33.7584
Offset  -7. Log likelihood = -33.0103
Offset  -6. Log likelihood = -33.1974
Offset  -5. Log likelihood = -34.7251
Offset  -4. Log likelihood = -33.6741
Offset  -3. Log likelihood = -32.8273
Offset  -2. Log likelihood = -33.0187
Offset  -1. Log likelihood = -32.9667
Offset   0. Log likelihood = -33.2824
Offset   1. Log likelihood = -34.2612
Offset   2. Log likelihood = -36.2365
Offset   3. Log likelihood = -36.4102
Offset   4. Log likelihood = -37.0889
Offset   5. Log likelihood = -42.7963
Offset   6. Log likelihood = -51.6521

Best offset -3. Log likelihood = -32.8273
Offset -3 means LFD numbers for week 2021-02-25 - 2021-03-03 are related to national case numbers in the week 2021-02-22 - 2021-02-28
Best estimate: LFDpos/LFDnum = 0.000115 + 0.777*(weekly case rate)
               where (weekly case rate) = (number of confirmed cases in a week) / 6.3e+06
False positive rate estimate: 0.011% (0.0048% - 0.018%)

Limitations

There is no absolute rule that says that true positives detected in schools by LFDs have to be proportional to cases detected in the country in the same age group. It seems like a very reasonable proposition, but it might not be right at low prevalence. For example, when cases are very low, people might get lax about swabbing, or they might tend to interpret marginal results as negatives because they believe that there is no virus around.

To the extent that this estimate is valid, it only properly applies to testing that is taking place in schools (the source of the data used here). Other tests or testers might have different swabbing techniques or they may treat a borderline reading differently, leading to a different sensitivity-specificity trade-off. Nevertheless, if this estimate is valid it would at least demonstrate that it is possible to obtain a very high specificity (by mimicking the schools' tests, techniques and procedures).

Whatever the false positive rate is now, it might be different from next week because children are now being tested at home, whereas at the point of collection of the data for this note, children were only being tested at school. This may make a difference since there will be a large number of tests that are not supervised by experienced staff and this may have an effect on the swabbing procedure or the interpretation of results. Also, the kind of people being tested will be different from a sampling point of view in that they can include symptomatic children. (When testing was only done at school, it shouldn't have included any symptomatic children, since if you are symptomatic you are not meant to leave your home.)

References

Code and data used here, 15 March 2021. https://github.com/alex1770/Covid-19/tree/LFDwriteup.2021-03-15/LFDevaluation
Crozier, A. et al. Put to the test: use of rapid testing technologies for covid-19, 3 February 2021. BMJ 2021;372:n208
Funk, S., Flasche, S. LFD mass testing in English schools - additional evidence of high test specificity, 5 March 2021. https://cmmid.github.io/topics/covid19/mass-testing-schools.html
UK coronavirus data api. New Cases By Publication Date.
Weekly statistics for NHS Test and Trace (England): 25 February to 3 March 2021, 11 March 2021. Tests conducted, table 7, taken from NHS Test and Trace weekly statistics)
Wolf, A., Hulmes, J., Hopkins, S. Lateral flow device specificity in phase 4 (post marketing) surveillance, DHSC, 10 March 2021. https://www.gov.uk/government/publications/lateral-flow-device-specificity-in-phase-4-post-marketing-surveillance

LFD specificity estimate