Difference between revisions of "The best strategies for Wordle"
| Line 138: | Line 138: | ||
(This is simplified for illustration. $$f()$$ should also depend on the number of remaining guesses. And in hard mode, $$T$$ will vary, so you need to carry it through $$f()$$ as $$f(T,H)$$ instead of just $$f(H)$$.) | (This is simplified for illustration. $$f()$$ should also depend on the number of remaining guesses. And in hard mode, $$T$$ will vary, so you need to carry it through $$f()$$ as $$f(T,H)$$ instead of just $$f(H)$$.) | ||
| − | How tractable this is will depend on how many intermediate subsets, $$H$$, we need to evaluate $$f()$$ on to get $$f(H_0)$$. Potentially there could be quite a lot of these. Naively, after five guesses there | + | How tractable this is will depend on how many intermediate subsets, $$H$$, we need to evaluate $$f()$$ on to get $$f(H_0)$$. Potentially there could be quite a lot of these. Naively, after five guesses there could be $$(12972\times243)^5$$ end nodes, but we can organise the search to avoid most of these. |
This is similar to a normal adversarial game, which would involve $$\min(\max(\min(\ldots)))$$, except that instead of the $$\max()$$ we have a sum. This is more awkward because there is less opportunity for an "alpha" cutoff, meaning it is not so easy to prove you can exit the $$\min$$ loop early. With min/max you'd be able to reason that there is no need to evaluate $$x$$ in expressions like $$\max(5, \min(4,x))$$, but here we have expressions like $$a+\min(b,x)$$ which will depend on $$x$$ for any finite values of $$a$$ and $$b$$. | This is similar to a normal adversarial game, which would involve $$\min(\max(\min(\ldots)))$$, except that instead of the $$\max()$$ we have a sum. This is more awkward because there is less opportunity for an "alpha" cutoff, meaning it is not so easy to prove you can exit the $$\min$$ loop early. With min/max you'd be able to reason that there is no need to evaluate $$x$$ in expressions like $$\max(5, \min(4,x))$$, but here we have expressions like $$a+\min(b,x)$$ which will depend on $$x$$ for any finite values of $$a$$ and $$b$$. | ||
Revision as of 01:24, 20 January 2022
The best strategies for Wordle
"What is the mathematically best way to play wordle?" - the burning question you never knew you wanted answered.
If you imagine you are up against a random allowable word, then the strategy that minimises the average number of guesses, in both normal and hard modes, starts with the guess SALET. If you continue always picking the best word, this will result in an average of 3.4212 guesses in normal mode and 3.5084 guesses in hard mode. Note: to be able to work this out, it's necessary to use an exact definition of the rules of the game. I've made some assumptions as to how they work in certain edge cases: see below, but I'm new to Wordle and might have got an assumption wrong, in which case the answers here could be wrong. I'd welcome any feedback on the precise rules.
To see how to play optimally, go to one of these strategy files: strategy in normal mode or strategy in hard mode, and see below for how to use them.
Of course there are different kinds of optimal play. If you prefer to minimise the worst-case number of guesses, then the answer is always five and there are many ways to achieve this. In normal mode, if you start with SALET then you can always guess the word within five attempts using the above strategy, but in hard mode starting with SALET will sometimes require you to use six guesses if you are unlucky. If you prefer to guarantee a maximum of five guesses, then in hard mode the best first guess is PALET and this is its strategy file.
| Rank | First word | Average guesses required | Total guesses required over all possible hidden words |
|---|---|---|---|
| 1 | SALET | 3.4212 | 7920 |
| 2 | REAST | 3.4225 | 7923 |
| =3 | CRATE | 3.4238 | 7926 |
| =3 | TRACE | 3.4238 | 7926 |
| 5 | SLATE | 3.4246 | 7928 |
| 6 | CRANE | 3.4255 | 7930 |
| 7 | CARLE | 3.4285 | 7937 |
| 8 | SLANE | 3.4311 | 7943 |
| 9 | CARTE | 3.4337 | 7949 |
| 10 | TORSE | 3.4341 | 7950 |
| Rank | First word | Average guesses required | Total guesses required over all possible hidden words |
|---|---|---|---|
| 1 | SALET | 3.5084 | 8122 |
| 2 | LEAST | 3.5106 | 8127 |
| 3 | REAST | 3.5136 | 8134 |
| 4 | CRATE | 3.5175 | 8143 |
| 5 | TRAPE | 3.5179 | 8144 |
| 6 | SLANE | 3.5201 | 8149 |
| 7 | PRATE | 3.5210 | 8151 |
| 8 | CRANE | 3.5227 | 8155 |
| =9 | TEALS | 3.5248 | 8160 |
| =9 | TRAIN | 3.5248 | 8160 |
How to use a strategy file
Start at the top left corner of the file, and enter that word as a guess. Then search in the file for the next match to the resulting scoring pattern with a '1' suffix. Then enter the word to the right of that. Then search in the file, from your current position, for the next match to the resulting scoring pattern with a '2' suffix. Repeat with a '3' suffix and so on, until you get five greens.
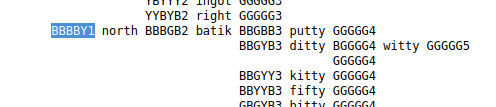
For example, working with the normal mode strategy, you would start with SALET, the word at the top,
which, let's say, returns a scoring pattern of BBBBY, meaning four blacks followed by a yellow. So then you search for BBBBY1 in the strategy file to arrive at this point,
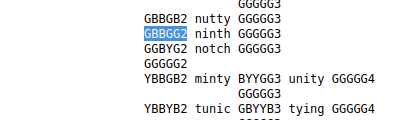
whereupon you would enter NORTH as your second guess. If that returned a scoring pattern of GBBGG then you would search from where you are in the file for GBBGG2.
As we can see, that means your final guess, guaranteed correct, would be NINTH.
Assumptions about the rules of Wordle
I think the colour scoring rules work like this, but would be happy to be corrected.
Let's refer to your guess as testword, and the secret word as hiddenword. Then I believe the scoring rules are these:
- First determine all greens, and cross out these letters in testword and hiddenword.
- Then from left to right in testword see which letters correspond to a letter in hiddenword. If you find one, then it's a yellow, but you need to cross it off in hiddenword.
- Remaining positions are scored as black.
The second point means that you can't reuse letters in hiddenword, so for example the total number of green 'T's and yellow 'T's in testword can't exceed the number of 'T's in hiddenword.
So if hiddenword is HOTEL then the testword SILLY would score BBYBB: the second 'L' does not score because only one 'L' can, and the earlier one takes precendence.
But if hiddenword were DAILY then the same testword SILLY would score BYBGG. This time it's the first 'L' that doesn't score, because even though it is earlier than the 'L' in fourth position, greens take priority over yellows.
The other slightly tricky rule is the one that determines what testwords are allowed in hard mode. Again, I think it works like this, but I would be happy for better information. The first condition is (obviously) that all greens from past guesses must be in their correct position in your testword. The second condition is, I assume, that your testword must have at least as many of each letter as implied by any past guess.
So for example, if a past guess were SILLY that scored BYYGB then that shows there are at least two 'L's in hiddenword (because of the non-letter-reusing feature of the scoring system mentioned above), and so each subsequent testword must have at least two 'L's, with one in position 4.
Note that, this does not require your testword be a possible hiddenword according to the previous guesses. In the above example you would be allowed to repeat the guess SILLY because it has enough 'I's and 'L's, despite not being a possible hiddenword because we know there can't be an 'I' in position 2 or an 'L' in position 3.
Description of algorithm
The programs used here are wordle.cpp and wordle-hard.cpp, available on github.
Wordle works with two wordlists, which can be found by inspecting the javascript of the Wordle page. There is a list of 2315 relatively common five-letter words, from which the hidden word of the day is chosen, and there is a larger list of 12972 five-letter words (which includes the smaller list) that can be used to guess with.
In fact the word of the day is chosen in a known sequence from the 2315, so it's easy to tell in advance what it will be. But there's no fun in that, which is why we're looking at how to deal with an unknown word.
Turning to the algorithm, this is one of those things where it's very quick to reach what you know is almost certainly the right answer to many questions (such as "Is this first word better than that one?"), because the heuristics are so reliable, but proving it takes much longer. The results on this web page are all meant to be proven correct (assuming no actual mistakes of course!) in the sense that (i) the list of the top 105 first words all have exact values derived from exhaustive search, and (ii) there are no other words of the 12972 that would score better than any on this list of 105, also established by a complete search.
The point of (i) is that there are fast incomplete searches that don't try every word at every stage, but are still very accurate. For example, in this list of estimated values of all 12972 first words, the large majority will be exactly right, and of those that aren't, the large majority will only be 1 too high, and of those that aren't, the large majority will be 2 too high, and so on. Or to take another example, the command wordle -n25 (an incomplete search which chooses from what it considers are the best 25 words at each point) will find SALET as the best choice in about 17 seconds on a single core (of my aging desktop machine), and estimate its value as 7921. wordle -n50 takes around 40 seconds and will find the correct value of 7920. By contrast, proving 7920 is the best value took about two days on a 6-core computer using the same program. (I have no doubt this can be improved, but it will still be a lot slower than the heuristic/partial search.)
Point (ii) is a bit more delicate: it's relatively easy to come up with a long list of exact values for first words, but it's harder to prove that no other words should be on that list. For example, this is a list of 3593 of good first words together with their proven exact values, but it took much less effort to find that than the certifiably complete top 105 list. The difference is the list of 105 is guaranteed to be exactly the best 105, but the list of 3593, though consisting of exact values, might be missing a few that would make the top 3593. (It is highly likely that the best 3500 of these 3593 are exactly the best 3500 out of all words, but this hasn't been proven.)
Moving on to some technical details... Let $$T$$ denote the set of all 12972 words that may be used as test words, and $$H_0$$ the set of all 2315 possible hidden words. We are interested in $$f(H_0)$$, the minimum over {all algorithms, $$A$$, for choosing test words based on previous guesses and scores} of $$\sum_{h\in H_0}A(h)$$, where $$A(h)$$ is how many guesses the algorithm would require if the hidden word were $$h$$. It's nicer to use a sum rather than an average here. ($$A(h)$$ can be taken to be infinity if it doesn't find $$h$$ within some prescribed number of guesses.)
Then $$f()$$ has a nice recursive definition. Let $$\text{score}(t,h)\in\{B,Y,G\}^5$$ denote the coloured 5-tuple from scoring testword $$t$$ against hidden word $$h$$. For $$s\in\{B,Y,G\}^5$$ and $$H\subset H_0$$, let $$P(H,t,s)=\{h\in H|\text{score}(t,h)=s\}$$, which collectively partition $$H$$ as $$s$$ varies. Then \[f(H)=\begin{cases} 0&\text{if } |H|=0 \\ 1 &\text{if } |H|=1 \\ |H|+\min_{t\in T}\sum_{s\neq \text{GGGGG}}f(P(H,t,s))&\text{otherwise.}\end{cases}\]
This is expressing the fact that, given you haven't discovered the hidden word yet, you are first going to have to use up a guess. Since we are summing over all possible hidden words, this results in the $$|H|$$ term, and since you get to pick the best test word you get to minimise over $$t\in T$$. Then if you happened to hit on the right answer you don't need to do anything else (the $$s\neq \text{GGGGG}$$ term), otherwise the colour-score of $$s$$ reduces your state of uncertainty about the hidden word from $$H$$ to $$P(H,t,s)$$.
(This is simplified for illustration. $$f()$$ should also depend on the number of remaining guesses. And in hard mode, $$T$$ will vary, so you need to carry it through $$f()$$ as $$f(T,H)$$ instead of just $$f(H)$$.)
How tractable this is will depend on how many intermediate subsets, $$H$$, we need to evaluate $$f()$$ on to get $$f(H_0)$$. Potentially there could be quite a lot of these. Naively, after five guesses there could be $$(12972\times243)^5$$ end nodes, but we can organise the search to avoid most of these.
This is similar to a normal adversarial game, which would involve $$\min(\max(\min(\ldots)))$$, except that instead of the $$\max()$$ we have a sum. This is more awkward because there is less opportunity for an "alpha" cutoff, meaning it is not so easy to prove you can exit the $$\min$$ loop early. With min/max you'd be able to reason that there is no need to evaluate $$x$$ in expressions like $$\max(5, \min(4,x))$$, but here we have expressions like $$a+\min(b,x)$$ which will depend on $$x$$ for any finite values of $$a$$ and $$b$$.
Still, we can make good use of the "beta" cutoff, which means we can exit the sum loop early, which is to say expressions like $$\min(5,6+x+y+z+...)$$ are independent of $$x$$, $$y$$, $$z$$, .... In an expression like $$\min(\beta, x+y+z+\ldots)$$ we can first evaluate fast lower bounds for all summands $$x, y, z, \ldots$$. If their sum exceeds $$\beta$$ then we're done. If not then we can set about strengthening the lower bounds in a suitable order, with the most promising summands re-evaluated first.
To evaluate the top 100 (say) first words, with proof that we have all of them, we can start by getting fast, and in practice very tight, upper bounds on the values of each word. We do this by restricting the $$\min$$ loop to the (e.g.,) 100 most promising words out of the 13972 available, arriving at this list. The score of the 100th best of these is 8014, so we can then re-evaluate all other candidate first words using a full run (allow all 13972 words at each stage, thereby ensuring exact answers) using a beta of 8015. This will distinguish all values under 8015, so it is guaranteed to fully evaluate all of the top 100 first words.
Other techniques in use include caching values of $$f(H)$$, and applying direct logic when $$H$$ can be solved within two guesses. I have no doubt there are other methods that could improve this a great deal further, but it seems a reasonable stopping point is when it is feasible to find the answer we wanted in a reasonable time (a day or two) on a single computer.
Top 105 first guesses in normal mode
| Rank | First word | Average guesses required | Total guesses required over all possible hidden words |
|---|---|---|---|
| 1 | SALET | 3.4212 | 7920 |
| 2 | REAST | 3.4225 | 7923 |
| =3 | CRATE | 3.4238 | 7926 |
| =3 | TRACE | 3.4238 | 7926 |
| 5 | SLATE | 3.4246 | 7928 |
| 6 | CRANE | 3.4255 | 7930 |
| 7 | CARLE | 3.4285 | 7937 |
| 8 | SLANE | 3.4311 | 7943 |
| 9 | CARTE | 3.4337 | 7949 |
| 10 | TORSE | 3.4341 | 7950 |
| 11 | SLANT | 3.4346 | 7951 |
| 12 | TRICE | 3.4350 | 7952 |
| 13 | LEAST | 3.4359 | 7954 |
| 14 | TRINE | 3.4367 | 7956 |
| 15 | PRATE | 3.4376 | 7958 |
| 16 | SLART | 3.4393 | 7962 |
| =17 | CARET | 3.4406 | 7965 |
| =17 | ROAST | 3.4406 | 7965 |
| 19 | STALE | 3.4415 | 7967 |
| 20 | RANCE | 3.4419 | 7968 |
| =21 | CLAST | 3.4423 | 7969 |
| =21 | LANCE | 3.4423 | 7969 |
| =21 | TRONE | 3.4423 | 7969 |
| 24 | CARSE | 3.4428 | 7970 |
| =25 | CRINE | 3.4436 | 7972 |
| =25 | TRAIN | 3.4436 | 7972 |
| =27 | EARST | 3.4445 | 7974 |
| =27 | STARE | 3.4445 | 7974 |
| 29 | TRADE | 3.4449 | 7975 |
| =30 | LEANT | 3.4454 | 7976 |
| =30 | ROIST | 3.4454 | 7976 |
| =30 | TRAPE | 3.4454 | 7976 |
| 33 | TASER | 3.4462 | 7978 |
| 34 | SNARE | 3.4471 | 7980 |
| =35 | PEART | 3.4475 | 7981 |
| =35 | REACT | 3.4475 | 7981 |
| 37 | SAINT | 3.4479 | 7982 |
| =38 | CRONE | 3.4488 | 7984 |
| =38 | TOILE | 3.4488 | 7984 |
| 40 | STANE | 3.4492 | 7985 |
| 41 | REIST | 3.4501 | 7987 |
| 42 | SCALE | 3.4505 | 7988 |
| 43 | PLATE | 3.4510 | 7989 |
| 44 | LOAST | 3.4514 | 7990 |
| =45 | CRISE | 3.4518 | 7991 |
| =45 | DRANT | 3.4518 | 7991 |
| 47 | RIANT | 3.4523 | 7992 |
| 48 | SOREL | 3.4527 | 7993 |
| =49 | CLART | 3.4531 | 7994 |
| =49 | ROSET | 3.4531 | 7994 |
| =49 | SANER | 3.4531 | 7994 |
| =52 | CORSE | 3.4540 | 7996 |
| =52 | SLICE | 3.4540 | 7996 |
| =54 | PARSE | 3.4544 | 7997 |
| =54 | SOARE | 3.4544 | 7997 |
| 56 | PLANE | 3.4549 | 7998 |
| 57 | ALIST | 3.4553 | 7999 |
| =58 | DEALT | 3.4557 | 8000 |
| =58 | ROATE | 3.4557 | 8000 |
| =58 | TARES | 3.4557 | 8000 |
| =61 | CROST | 3.4562 | 8001 |
| =61 | RESAT | 3.4562 | 8001 |
| =63 | ALINE | 3.4566 | 8002 |
| =63 | ARTEL | 3.4566 | 8002 |
| =63 | CANST | 3.4566 | 8002 |
| =63 | LIANE | 3.4566 | 8002 |
| =63 | RONTE | 3.4566 | 8002 |
| =63 | STILE | 3.4566 | 8002 |
| =69 | PRASE | 3.4570 | 8003 |
| =69 | RAINE | 3.4570 | 8003 |
| =69 | STORE | 3.4570 | 8003 |
| =69 | TRIED | 3.4570 | 8003 |
| =73 | ANTRE | 3.4575 | 8004 |
| =73 | TRIPE | 3.4575 | 8004 |
| =75 | CANER | 3.4579 | 8005 |
| =75 | RAILE | 3.4579 | 8005 |
| =75 | SAULT | 3.4579 | 8005 |
| =78 | ORANT | 3.4583 | 8006 |
| =78 | SAINE | 3.4583 | 8006 |
| =78 | STRAE | 3.4583 | 8006 |
| =78 | TEARS | 3.4583 | 8006 |
| =78 | TRAIL | 3.4583 | 8006 |
| =83 | ORATE | 3.4592 | 8008 |
| =83 | SNIRT | 3.4592 | 8008 |
| =83 | STOLE | 3.4592 | 8008 |
| =83 | THALE | 3.4592 | 8008 |
| =83 | TRUCE | 3.4592 | 8008 |
| 88 | CLOSE | 3.4596 | 8009 |
| 89 | CATER | 3.4600 | 8010 |
| =90 | AROSE | 3.4605 | 8011 |
| =90 | CLINE | 3.4605 | 8011 |
| =90 | CREST | 3.4605 | 8011 |
| =90 | EARNT | 3.4605 | 8011 |
| =94 | ALTER | 3.4609 | 8012 |
| =94 | SERAL | 3.4609 | 8012 |
| =94 | TRANS | 3.4609 | 8012 |
| =97 | LIART | 3.4613 | 8013 |
| =97 | PLACE | 3.4613 | 8013 |
| =97 | SNORE | 3.4613 | 8013 |
| =100 | GRATE | 3.4618 | 8014 |
| =100 | RAISE | 3.4618 | 8014 |
| =100 | RINSE | 3.4618 | 8014 |
| =100 | SLADE | 3.4618 | 8014 |
| =100 | SPALT | 3.4618 | 8014 |
| =100 | TALER | 3.4618 | 8014 |
Top 101 first guesses in hard mode
| Rank | First word | Average guesses required | Total guesses required over all possible hidden words |
|---|---|---|---|
| 1 | SALET | 3.5084 | 8122 |
| 2 | LEAST | 3.5106 | 8127 |
| 3 | REAST | 3.5136 | 8134 |
| 4 | CRATE | 3.5175 | 8143 |
| 5 | TRAPE | 3.5179 | 8144 |
| 6 | SLANE | 3.5201 | 8149 |
| 7 | PRATE | 3.5210 | 8151 |
| 8 | CRANE | 3.5227 | 8155 |
| =9 | TEALS | 3.5248 | 8160 |
| =9 | TRAIN | 3.5248 | 8160 |
| 11 | CARLE | 3.5261 | 8163 |
| =12 | DEALT | 3.5274 | 8166 |
| =12 | TRICE | 3.5274 | 8166 |
| =14 | REIST | 3.5283 | 8168 |
| =14 | TRINE | 3.5283 | 8168 |
| 16 | STALE | 3.5292 | 8170 |
| 17 | ALIST | 3.5296 | 8171 |
| =18 | CLAST | 3.5305 | 8173 |
| =18 | TORSE | 3.5305 | 8173 |
| =18 | TRADE | 3.5305 | 8173 |
| =18 | TRAIL | 3.5305 | 8173 |
| 22 | PEART | 3.5309 | 8174 |
| 23 | TRIPE | 3.5326 | 8178 |
| =24 | SLART | 3.5330 | 8179 |
| =24 | TRONE | 3.5330 | 8179 |
| 26 | EARST | 3.5335 | 8180 |
| =27 | LANCE | 3.5343 | 8182 |
| =27 | PALET | 3.5343 | 8182 |
| =29 | ALERT | 3.5348 | 8183 |
| =29 | PLATE | 3.5348 | 8183 |
| 31 | CARSE | 3.5352 | 8184 |
| 32 | PLANE | 3.5356 | 8185 |
| =33 | TAELS | 3.5374 | 8189 |
| =33 | TALES | 3.5374 | 8189 |
| =35 | CLART | 3.5382 | 8191 |
| =35 | TARNS | 3.5382 | 8191 |
| =35 | TRIAL | 3.5382 | 8191 |
| 38 | PLAST | 3.5387 | 8192 |
| 39 | TEARS | 3.5391 | 8193 |
| =40 | ARTEL | 3.5404 | 8196 |
| =40 | DRANT | 3.5404 | 8196 |
| =42 | SCALE | 3.5413 | 8198 |
| =42 | SPALT | 3.5413 | 8198 |
| =44 | CLEAT | 3.5417 | 8199 |
| =44 | LEAPT | 3.5417 | 8199 |
| =44 | ROIST | 3.5417 | 8199 |
| =44 | SETAL | 3.5417 | 8199 |
| =44 | TESLA | 3.5417 | 8199 |
| =49 | LOAST | 3.5421 | 8200 |
| =49 | PRASE | 3.5421 | 8200 |
| =49 | TOILE | 3.5421 | 8200 |
| 52 | TRIES | 3.5425 | 8201 |
| =53 | ROAST | 3.5430 | 8202 |
| =53 | TAILS | 3.5430 | 8202 |
| 55 | LATEN | 3.5434 | 8203 |
| =56 | LACET | 3.5438 | 8204 |
| =56 | TALER | 3.5438 | 8204 |
| =58 | SCART | 3.5443 | 8205 |
| =58 | TASER | 3.5443 | 8205 |
| =60 | CROST | 3.5451 | 8207 |
| =60 | PERST | 3.5451 | 8207 |
| =60 | PLACE | 3.5451 | 8207 |
| =60 | TRANS | 3.5451 | 8207 |
| =60 | TRIED | 3.5451 | 8207 |
| =65 | PLAIT | 3.5456 | 8208 |
| =65 | STARE | 3.5456 | 8208 |
| =67 | ANTRE | 3.5460 | 8209 |
| =67 | PARSE | 3.5460 | 8209 |
| =67 | TIRES | 3.5460 | 8209 |
| =70 | SPALE | 3.5464 | 8210 |
| =70 | TRIOL | 3.5464 | 8210 |
| 72 | TALON | 3.5469 | 8211 |
| =73 | SERAL | 3.5473 | 8212 |
| =73 | TORAN | 3.5473 | 8212 |
| =75 | CRONE | 3.5477 | 8213 |
| =75 | LIART | 3.5477 | 8213 |
| =75 | TRIDE | 3.5477 | 8213 |
| =78 | LEARN | 3.5482 | 8214 |
| =78 | ROATE | 3.5482 | 8214 |
| =80 | LEANS | 3.5486 | 8215 |
| =80 | SLIPT | 3.5486 | 8215 |
| =80 | SNORT | 3.5486 | 8215 |
| =80 | TARES | 3.5486 | 8215 |
| =80 | TERAS | 3.5486 | 8215 |
| =85 | ALTER | 3.5490 | 8216 |
| =85 | TEILS | 3.5490 | 8216 |
| =85 | TILES | 3.5490 | 8216 |
| =88 | RATEL | 3.5495 | 8217 |
| =88 | TARED | 3.5495 | 8217 |
| =90 | ALIEN | 3.5499 | 8218 |
| =90 | ORATE | 3.5499 | 8218 |
| =90 | SNARE | 3.5499 | 8218 |
| =93 | CLOTE | 3.5503 | 8219 |
| =93 | PREST | 3.5503 | 8219 |
| =93 | TROPE | 3.5503 | 8219 |
| =96 | ANCLE | 3.5508 | 8220 |
| =96 | DERAT | 3.5508 | 8220 |
| =96 | PLEAT | 3.5508 | 8220 |
| =96 | RONTE | 3.5508 | 8220 |
| =96 | SPATE | 3.5508 | 8220 |
| =96 | STOLE | 3.5508 | 8220 |