Gomes

Article

Note on "Individual variation in susceptibility or exposure to SARS-CoV-2 lowers the herd immunity threshold" by M. Gabriella M. Gomes et al.

This paper made a media splash early in May 2020 with headlines such as "Herd immunity may only need 10-20 per cent of people to be infected". The proposed mechanism is that people who are more susceptible to the infection are those more involved in spreading it, but will also become immune at a faster rate than others, so the disease naturally tends to make the key players immune more so than others.

Discussion

• This paper uses two variants of a standard SEIR model. The first is the "susceptibility model", where the population is divided into classes according to a parameter that governs to what extent they are likely to become infected. Passing on the infection is still assumed to occur uniformly. The second is the "connectivity model" which takes this further by assuming that infectivity is proportional to susceptibility. I suppose the latter model is called "connectivity" because it is equivalent to changing the connectivity of the underlying graph - making it random subject to a degree distribution. Note that throughout, the term "susceptibility" refers to the potential to catch the disease, not the severity of outcome.

• Varying the infectivity alone would just reduce to a standard SEIR model because everyone (all infectivity classes) would be being infected at the same rate. By contrast, in the two above models the susceptibility classes are being depleted at different rates from each other.

• As the authors conclude, there is an effect where the herd immunity threshold (HIT) in the two models above is lower than that predicted by simple homogeneous modelling ($$1-1/R_0$$). This is a valuable point to make given that some seem to be taking as read that the herd immunity threshold must be 60-70%, and we obviously very much need to know when herd immunity arises, or at least to what extent we should expect to feel the effects of partial herd immunity. (Though the idea that the HIT is lower in the presence of heterogeneity will of course be familiar to epidemiologists.)

• I doubt that a HIT as low as 10% is at all likely. It arises in this paper's model from an extreme distribution of susceptibilities where there is a big concentration at the low end. I couldn't find any evidence presented in the paper for a particular distribution, or a particular variance, for any given susceptibility distibution. There are references to sources which give evidence or arguments for a certain distribution (or dispersion) of individual infectivities, and it seems the authors of the present paper intend this to inform the distribution of individual susceptibilities, but I think this is a different thing. Of course, the present authors are aware of this, but as there is scant information to go on they are just making the best use of what there is. (More on this below.)

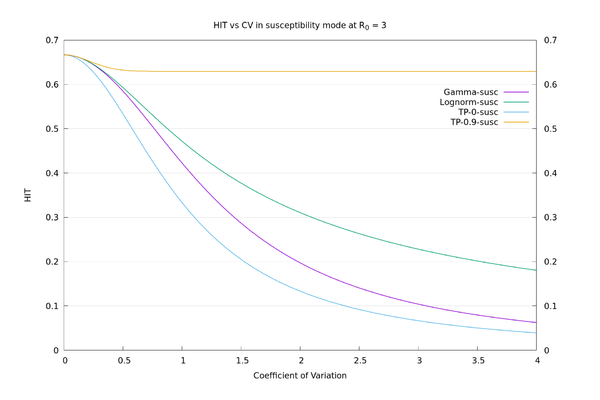
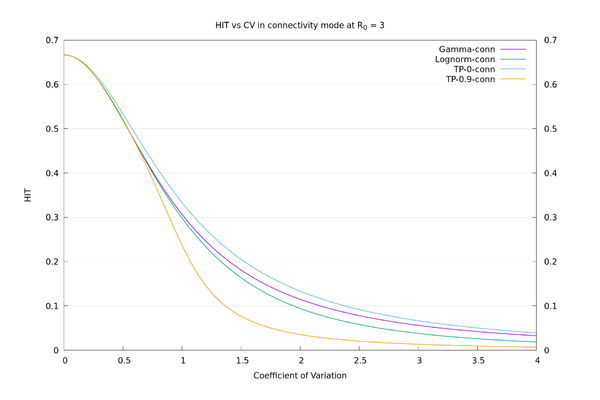
• Contrary to the practice in the paper, I believe the Coefficient of Variation (CV), or other dispersion parameter that is basically a function of the mean and variance, is not, for these purposes, a suitable parameter to use to measure how much the susceptibility distribution varies from a point value (constant). To demonstrate this we can choose different (hypothetical) distributions with the same CV and get a huge range of HITs.

• There is actually a nice clean way to evaluate the HIT directly from the susceptibility distribution under the given models.

• In their model, social distancing / locking down only affects the overall time parameter. It's unclear how realistic this is, but under this model one could decouple the question of what the HIT is, with how to manage (by distancing etc.) the flow of the disease. As such, the focus is mainly on what the HIT is.

• The present paper shows what happens if you "artificially" add in a variation in susceptibility, i.e., treat everyone uniformly except for a susceptibility parameter controlled by a given distribution. An alternative approach would be to use a real life contact graph, or some version of it. Age- and location-based contact information have been studied for this purpose, e.g., Prem et al and Klepac et al. Such a calculation is carried out in Bitton et al using Age- and Activity-based mixing matrices. They find, inter alia, that if $$R_0=3$$ then the HIT is reduced from $$66.7%$$ to $$49.1%$$. This empirically-derived distribution has the merit of being justifiable, but (and I'm speculating here) I wonder if it understates the full heterogeneity, in which case there might be an argument for trying a hybrid method where you artificially introduce a little more variability (somehow calibrated to reality), maybe in the manner of the present paper, on top of the empirically-found mixing matrices.

In more detail

The lowest HIT estimates in this paper arise from using a Gamma distribution with $$CV=3$$ for the susceptibility distribution, which corresponds to shape parameter $$k=1/9$$. This has a large chunk of its probability at the very low end: it is saying that 63% of the population has susceptibility less than 0.09 (relative to a mean of 1) and 50% has susceptibility less than 0.01. With this in mind, it's not surprising that we end up with low HIT estimates because, roughly speaking, in this case you only need to induce herd immunity amongst the minority susceptible population.

Note that a similar-sounding argument to this is not correct: if the infectivities, but not susceptibilities, were clustered near 0 then it would still be true that you only need to induce herd immunity amongst the minority infective population, but that wouldn't occur naturally because the infective portion of the population wouldn't be getting infected any more than the non-infective portion.

There is some evidence that infectivity is strongly clustered like this (and has a long tail - i.e., superspreaders). The present paper cites Endo et al that suggests a dispersion of something like $$k=1/10$$ in SARS-CoV-2. This relies (slightly optimistically in my opinion) on knowledge of the seed infections in different countries to derive its result, but perhaps more importantly this cited paper is making a statement about infectivity not susceptibility. Also cited is the classic 2005 paper Lloyd-Smith et al on superspreading for the original SARS outbreak. This estimates a dispersion parameter of $$k=0.16$$ and also gives evidence that the Gamma family is a good one to use (because a Poisson with parameter Gamma is a Negative Binomial, and they find evidence for the Negative Binomial family being a good description), but again this is talking about infectivity not susceptibility so I believe this isn't directly applicable to the situation of the present paper.

Regardless of the somewhat shaky evidence, is it yet possible that the real susceptibility distribution looks like a Gamma with shape $$1/9$$? I suspect this is unlikely. As far as I am aware anyone can catch the disease, and there aren't any known huge differences in susceptibility to catching the disease amongst subpopulations. The best candidate might be age, since the disease is so strongly age-dependent in terms of severity, but while young people may be a little less susceptible to catching it, it's clearly (from any prevalence survey you look at) far from true that the younger 50% of the population (median age in the UK is 40.5 years) are less than $$1/100$$ as susceptible to catching it compared with the average. Or if susceptibility variation is mainly arising from connectivity, then a shape $$1/9$$ Gamma distribution is still not right because it's clearly not the case (in normal times, which is what we are talking about here, since we are investigating the question of herd immunity after dropping restrictions) that more than 50% of the population lives alone and essentially never meets anyone at all. Arguments against lower $$CV$$ become progressively less clear cut - I won't pursue this further.

To illustrate how the HIT doesn't properly depend on $$CV$$, I tried using a "two-point" distribution parameterized by $$x, y$$ and $$p$$, where $$P(X=x)=p$$, and $$P(X=y)=1-p$$. Fixing the mean to be 1 and the variance to be $$CV^2$$ leaves a free parameter that may as well be $$x$$, and I look at the opposite extremes of $$x=0$$ and $$x=0.9$$. There are superspreaders in both of these cases (though more extreme in the $$x=0.9$$ case), but the $$x=0$$ case also has a lot of (for want of a better term) "superhermits" - i.e., like Gamma at $$CV=3$$, lots of the distribution is concentrated at or near 0. Of course these distributions are unrealistic as real-world examples. They are just there to make the point that $$CV$$ isn't a good characterisation of spread for the purposes of calculating the HIT.

(To help my understanding, and to check the paper, I reimplemented their models in Python. This gives a good match to the output of version 1 of their paper in "susceptibility" mode, though not in "connectivity" mode. Possibly the discrepancy in the latter mode is due to a difference in our initial conditions. In any case there is only a discrepancy in the progress of the infection, not in the HITs, which are anyway separately calculable - see below.)

Version 2 of the paper came out after I tried these examples, and in it the authors also try out a different family of distributions (lognormal) to test robustness and dependence of their results on a particular family (Gamma). Using lognormal they do in fact get much bigger answers for the HIT than they do for Gamma in the $$CV=3$$ case, but as far as I can see this is not mentioned in the main body of their paper. It's also relevant that the lognormal family doesn't have a free parameter to vary like the two-point distribution has, so you can't make it particularly extreme like you can with the two-point family.

As an illustration, the HIT values for the four distributions, in "susceptibility" mode at $$R_0=3$$, all with $$CV=3$$, are: Two-point at x=0: 6.7%, Gamma: 10.4%, Lognormal: 22.3%, Two-point at x=0.9: 63.0%. We see there is a large variation in HIT for the same $$CV$$, so it doesn't make sense to think of HIT as a function of $$CV$$. In "connectivity" mode the values are more consistent: Two-point at x=0: 6.7%, Gamma: 5.6%, Lognormal: 3.8%, Two-point at x=0.9: 1.3%. See also the graphs below.

Appendix - direct formulae

As it happens, there is a nice clean procedure to directly calculate the HIT under the authors' model, so there is no need for simulation, and there is no dependency of on particular characteristics such as the timing of the switching on and off of social distancing. (The reason for this is that $$S_t(x)=S_0(x)e^{-\Lambda(t)x}$$. That is, the $$t-$$dependence and $$x-$$dependence decouple.) I don't think the authors used this.

For the Gamma family there happens to be a closed-form formula. Using the "susceptibility" model it's

\[\text{HIT} = 1-R_0^{-(1+CV^2)^{-1}},\] and with the "connectivity" model it's

\[\text{HIT} = 1-R_0^{-(1+2CV^2)^{-1}}.\]

In general the procedure for any distribution of initial susceptibilities/connectivities, written as the random variable $$X$$ with $$E[X]=1$$, is as follows:

• Susceptibility: choose $$\Lambda\ge0$$ such that $$R_0 E[Xe^{-\Lambda X}]=1$$, then $$\text{HIT}=1-E[e^{-\Lambda X}]$$.

• Connectivity: choose $$\Lambda\ge0$$ such that $$R_0 E[X^2e^{-\Lambda X}]=E[X^2]$$, then $$\text{HIT}=1-E[e^{-\Lambda X}]$$.

(If you need a susceptibility distribution with $$E[X]\neq1$$, and also want to keep the notation of this paper, and want $$R_0$$ to retain its conventional meaning of the initial branching factor, then you need to absorb the factor of $$E[X]$$ into $$R_0$$ and rescale $$X$$ to have mean 1.)

We may now compare the solid curves from the paper of fig.3 (HIT as a function of $$CV$$ assuming Gamma distribution), and those of fig. S22 (HIT as a function of $$CV$$ assuming lognormal distribution), with those given by the above procedure. We also add in the two-point $$x=0$$ and two-point $$x=0.9$$ distributions for comparison. It can be seen that there is a wide variation in behaviour for a given $$CV$$, depending on what distribution is used.