Difference between revisions of "SuppressionStrategy"
| (8 intermediate revisions by the same user not shown) | |||
| Line 15: | Line 15: | ||
\[R=e^{\lambda T}.\] | \[R=e^{\lambda T}.\] | ||
| − | But because the time taken to infect someone is not a constant, a better formula is | + | But because the time taken to infect someone is not a constant, [https://plus.maths.org/content/epidemic-growth-rate a better formula] is |
\[R=r(\lambda)=\mathbb E[e^{-\lambda X}]^{-1},\] | \[R=r(\lambda)=\mathbb E[e^{-\lambda X}]^{-1},\] | ||
| Line 21: | Line 21: | ||
where $$X$$ is the time to infection for each infectee, considered as a random variable. (Note, the above expectation uses a different probability space from that considered next.) | where $$X$$ is the time to infection for each infectee, considered as a random variable. (Note, the above expectation uses a different probability space from that considered next.) | ||
| − | Consider the reproduction rate $$R$$ to be a random variable satisfying $$0<R\le R_0$$. Our goal (imagining ourselves to be the government) is to choose the best distribution for $$R$$. Here $$R_0$$ is the usual reproduction number in the absence of any distancing measures, which serves as an upper bound for $$R$$ under distancing. For example, $$\mathbb P(1<R<2)=1/4$$ would mean that we want be spending $$1/4$$ of the time with $$R$$ between $$1$$ and $$2$$. Let us suppose there is some utility function $$U(R)$$, increasing in $$R$$, that represents the benefit to society of maintaining a constant reproduction of $$R$$. Additive constants don't matter to $$U()$$, so it may be helpful to think of $$U(R)$$ negative and increasing up to $$U(R_0)=0$$. $$R=R_0$$ represents normal life in the absence of a pandemic, while negative $$U(R)$$ for $$R<R_0$$ represents the level of pain at implementing various levels of distancing/lockdown. Note that $$U(R)$$ is the utility when you fix the reproduction number at $$R$$; the possibility of varying this is what we're going to look at here and is represented by a mixture of different values of $$U()$$. For example, the strategy described in the preceding paragraph would have value $$\frac13(U(4)+2U(\frac12))$$. It seems reasonable that there is some version of the function $$U()$$ that represents reality to some extent, though of course it will be hard to agree upon any particular version of $$U()$$. We shall therefore try to see what we can deduce that doesn't depend on a precise $$U()$$, starting with observations that are more-or-less completely $$U()$$-independent, and ending with speculation that depends on a broad form of $$U()$$. | + | Consider the reproduction rate $$R$$ to be a random variable satisfying $$0<R\le R_0$$. Our goal (imagining ourselves to be the government) is to choose the best distribution for $$R$$. Here $$R_0$$ is the usual reproduction number in the absence of any distancing measures, which serves as an upper bound for $$R$$ under distancing. For example, $$\mathbb P(1<R<2)=1/4$$ would mean that we want be spending $$1/4$$ of the time with $$R$$ between $$1$$ and $$2$$. Let us suppose there is some utility function $$U(R)$$, increasing in $$R$$, that represents the benefit to society of maintaining a constant reproduction of $$R$$. For these purposes we'll assume that $$U()$$ is time-independent, though this isn't entirely realistic as seasonal factors, for example, will influence transmission rates and so how painful certain suppression measures are. Additive constants don't matter to $$U()$$, so it may be helpful to think of $$U(R)$$ negative and increasing up to $$U(R_0)=0$$. $$R=R_0$$ represents normal life in the absence of a pandemic, while negative $$U(R)$$ for $$R<R_0$$ represents the level of pain at implementing various levels of distancing/lockdown. Note that $$U(R)$$ is the utility when you fix the reproduction number at $$R$$; the possibility of varying this is what we're going to look at here and is represented by a mixture of different values of $$U()$$. For example, the strategy described in the preceding paragraph would have value $$\frac13(U(4)+2U(\frac12))$$. It seems reasonable that there is some version of the function $$U()$$ that represents reality to some extent, though of course it will be hard to agree upon any particular version of $$U()$$. We shall therefore try to see what we can deduce that doesn't depend on a precise $$U()$$, starting with observations that are more-or-less completely $$U()$$-independent, and ending with speculation that depends on a broad form of $$U()$$. |
For these purposes it's more convenient to work with the growth rate $$\lambda$$, which we can consider as a random variable $$\Lambda$$ related to $$R$$ by $$R=r(\Lambda)$$. However, we shall also keep $$R$$ in the picture because it's probably more intuitive to people now as we've had experience of reproduction rates in the news. Using growth rate as the random variable, we can define $$V(\lambda)=U(r(\lambda))$$ and formulate the problem like this: | For these purposes it's more convenient to work with the growth rate $$\lambda$$, which we can consider as a random variable $$\Lambda$$ related to $$R$$ by $$R=r(\Lambda)$$. However, we shall also keep $$R$$ in the picture because it's probably more intuitive to people now as we've had experience of reproduction rates in the news. Using growth rate as the random variable, we can define $$V(\lambda)=U(r(\lambda))$$ and formulate the problem like this: | ||
| Line 35: | Line 35: | ||
$$V()$$ is some increasing function and $$\Lambda\le\Lambda_0$$, where $$\Lambda_0$$ is defined by $$r(\Lambda_0)=R_0$$. This is meant to capture the time-independent aspect of the problem of medium/long term control of the virus: decide how long you want to spend at different lockdown levels, and factor out "implementation details" of how/when to switch from one level to another. Obviously in reality such "details" are very important and may in practice be a sticking point but still I think it's interesting to consider what kinds of distributions are likely to make sense. | $$V()$$ is some increasing function and $$\Lambda\le\Lambda_0$$, where $$\Lambda_0$$ is defined by $$r(\Lambda_0)=R_0$$. This is meant to capture the time-independent aspect of the problem of medium/long term control of the virus: decide how long you want to spend at different lockdown levels, and factor out "implementation details" of how/when to switch from one level to another. Obviously in reality such "details" are very important and may in practice be a sticking point but still I think it's interesting to consider what kinds of distributions are likely to make sense. | ||
| − | Note that we don't consider the possibility of $$\mathbb E[\Lambda]<0$$ even though this would also result in disease suppression, because $$V()$$ is increasing so if $$-\infty<E[\Lambda]<0$$ we may as well increase $$\Lambda$$ a bit to improve $$\E[V(\Lambda)]$$ and maintain suppression. And $$\mathbb E[\Lambda]=-\infty$$ is a zero-Covid strategy (leading to extinction of the disease) which we are not considering here, so in particular we must have $$\mathbb P(\Lambda=-\infty)=\mathbb P(R=0)=0$$. | + | Note that we don't consider the possibility of $$\mathbb E[\Lambda]<0$$ even though this would also result in disease suppression, because $$V()$$ is increasing so if $$-\infty<\mathbb E[\Lambda]<0$$ we may as well increase $$\Lambda$$ a bit to improve $$\mathbb E[V(\Lambda)]$$ and maintain suppression. And $$\mathbb E[\Lambda]=-\infty$$ is a zero-Covid strategy (leading to extinction of the disease) which we are not considering here, so in particular we must have $$\mathbb P(\Lambda=-\infty)=\mathbb P(R=0)=0$$. |
= Only two values of $$R$$ are needed = | = Only two values of $$R$$ are needed = | ||
| − | Equivalently, only two values of $$\Lambda$$ are needed. Suppose that $$\Lambda$$ only takes finitely many values: $$\mathbb P(\Lambda=\lambda_i)=p_i$$ for $$i=1,\ldots, n$$, where $$p_i>0$$ and $$0<r_1<\ldots<r_n$$. If $$n\ge3$$ then we can consider the effect of adjusting the probabilities $$(p_1, p_2, p_3)$$ by a multiple of $$(\Delta p_1, \Delta p_2, \Delta p_3)=(\lambda_2-\lambda_3, \lambda_3-\lambda_1, \lambda_1-\lambda_2)$$ since that preserves $$\sum_i p_i$$ and $$\sum_i p_i\lambda_i$$. If $$\Delta V = V(\lambda_1)\Delta p_1+V(\lambda_2)\Delta p_2+V(\lambda_3)\Delta p_3\ge0$$ then we can improve the overall value by adding on a positive multiple of $$(\Delta p_1, \Delta p_2, \Delta p_3)$$, while if $$\Delta V\le0$$ we can use a negative multiple. Either way we can change $$p_1, p_2, p_3$$ until one of them becomes $$0$$. This demonstrates that we only need to consider $$n=1$$ or $$n=2$$. | + | Equivalently, only two values of $$\Lambda$$ are needed. Suppose that $$\Lambda$$ only takes finitely many values (which isn't a very onerous restriction): $$\mathbb P(\Lambda=\lambda_i)=p_i$$ for $$i=1,\ldots, n$$, where $$p_i>0$$ and $$0<r_1<\ldots<r_n$$. If $$n\ge3$$ then we can consider the effect of adjusting the probabilities $$(p_1, p_2, p_3)$$ by a multiple of $$(\Delta p_1, \Delta p_2, \Delta p_3)=(\lambda_2-\lambda_3, \lambda_3-\lambda_1, \lambda_1-\lambda_2)$$ since that preserves $$\sum_i p_i$$ and $$\sum_i p_i\lambda_i$$. If $$\Delta V = V(\lambda_1)\Delta p_1+V(\lambda_2)\Delta p_2+V(\lambda_3)\Delta p_3\ge0$$ then we can improve the overall value by adding on a positive multiple of $$(\Delta p_1, \Delta p_2, \Delta p_3)$$, while if $$\Delta V\le0$$ we can use a negative multiple. Either way we can change $$p_1, p_2, p_3$$ until one of them becomes $$0$$. This demonstrates that we only need to consider $$n=1$$ or $$n=2$$. |
This is slightly interesting. Based only on fairly mild assumptions, it means you only want to be aiming for at most two states: relatively locked down or relatively relaxed (or with $$n=1$$, aim for just one state), and not using anything in between. Of course this is only absolutely true within the idealisation we have used and doesn't automatically invalidate the multi-tiered approach which many countries have adopted. In the real world you don't know exactly what $$R$$ you will get from a particular set of measures, so it may be useful to have a responsive set of measures that are able to nudge $$R$$ down or up a bit. | This is slightly interesting. Based only on fairly mild assumptions, it means you only want to be aiming for at most two states: relatively locked down or relatively relaxed (or with $$n=1$$, aim for just one state), and not using anything in between. Of course this is only absolutely true within the idealisation we have used and doesn't automatically invalidate the multi-tiered approach which many countries have adopted. In the real world you don't know exactly what $$R$$ you will get from a particular set of measures, so it may be useful to have a responsive set of measures that are able to nudge $$R$$ down or up a bit. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
= Should we use 1 or 2 values of $$R$$? = | = Should we use 1 or 2 values of $$R$$? = | ||
| Line 99: | Line 86: | ||
For an example of a strong/weak policy, one could combine the $$R=1.4$$ state in mid-September at the height of the loosening with $$R=0.8$$ of May (or possibly November during "Lockdown 2"). This would have to be taken in the ratio of something like 1:2, for example one month of $$R=1.4$$ followed by two of $$R=0.8$$. The [https://web.archive.org/web/20200520063031/https://www.gov.uk/government/publications/coronavirus-outbreak-faqs-what-you-can-and-cant-do/coronavirus-outbreak-faqs-what-you-can-and-cant-do restrictions in place on 20 May 2020 can be found here] while [https://web.archive.org/web/20200909063459/https://www.gov.uk/government/publications/coronavirus-outbreak-faqs-what-you-can-and-cant-do/coronavirus-outbreak-faqs-what-you-can-and-cant-do those in place on 13 September 2020 can be found here]. | For an example of a strong/weak policy, one could combine the $$R=1.4$$ state in mid-September at the height of the loosening with $$R=0.8$$ of May (or possibly November during "Lockdown 2"). This would have to be taken in the ratio of something like 1:2, for example one month of $$R=1.4$$ followed by two of $$R=0.8$$. The [https://web.archive.org/web/20200520063031/https://www.gov.uk/government/publications/coronavirus-outbreak-faqs-what-you-can-and-cant-do/coronavirus-outbreak-faqs-what-you-can-and-cant-do restrictions in place on 20 May 2020 can be found here] while [https://web.archive.org/web/20200909063459/https://www.gov.uk/government/publications/coronavirus-outbreak-faqs-what-you-can-and-cant-do/coronavirus-outbreak-faqs-what-you-can-and-cant-do those in place on 13 September 2020 can be found here]. | ||
| − | (*) It's common to use the [https://en.wikipedia.org/wiki/Gamma_distribution Gamma distribution] here because it's a very convenient two-parameter family of non-negative distributions, not because there is a particular reason to expect the distribution to have this precise form. (And there isn't usually enough data to fit more than two parameters.) If $$X\sim\Gamma(\alpha,\beta)$$ then $$V(\lambda)=U(\theta^\alpha)$$, where $$\theta=1+(\alpha/\beta)\lambda$$, and $$V''(\lambda)=(\alpha/\beta)^2\theta^{2\alpha-2}U''(\theta^\alpha)+(\alpha(\alpha-1)/\beta^2)\theta^{\alpha-2}U'(\theta^\alpha)$$, so provided $$\alpha>1$$ which is what everyone thinks, then $$V()$$ is more convex than $$U()$$ because $$V''$$ has an extra term that is always positive. | + | However, if the strongest lockdown we can manage only has $$R$$ as low as $$0.7-0.8$$, which is what we've managed hitherto, then intuition suggests that the benefits of a two-level strategy are probably not that great. Roughly speaking, if you do something like mix $$R=0.8$$ with $$R=1.25$$ in equal proportions then the average $$R$$ value (a proxy for the overall benefit) is only $$1.025$$. You'd get a more useful gain if you could mix something like $$R=0.5$$ with $$R=2$$ for an average $$R$$ of $$1.25$$ (we should really be working with growth not $$R$$, but this is just a rough thought), though I don't know if an $$R=0.5$$ regime is practically possible. |
| + | |||
| + | (*) It's common to use the [https://en.wikipedia.org/wiki/Gamma_distribution Gamma distribution] here because it's a very convenient two-parameter family of non-negative distributions, not because there is a particular reason to expect the distribution to have this precise form. (And there isn't usually enough data to fit more than two parameters.) If $$X\sim\Gamma(\alpha,\beta)$$ then $$V(\lambda)=U(\theta^\alpha)$$, where $$\theta=1+(\alpha/\beta)\lambda$$, and $$V''(\lambda)=(\alpha/\beta)^2\theta^{2\alpha-2}U''(\theta^\alpha)+(\alpha(\alpha-1)/\beta^2)\theta^{\alpha-2}U'(\theta^\alpha)$$, so provided $$\alpha>1$$, which is what everyone thinks, then $$V()$$ is "more convex" than $$U()$$ because $$V''$$ has an extra term that is always positive. | ||
| + | |||
| + | = An alternative (and simpler) argument = | ||
| + | |||
| + | Given a period of $$R=R_1$$ for time $$T_1$$ followed by a period of $$R=R_2$$ for time $$T_2$$, then swapping these two periods around (doing $$R=R_2$$ for time $$T_2$$ first) doesn't change anything before or after the two periods. At least, this is true in the idealisation we've been considering here where the policy in each period multiplies the disease prevalence by a factor independent of the incoming prevalence: granted this, it doesn't matter which order we multiply these two factors. But during the two periods, it's better to take the smaller $$R$$ first since you'd then enjoy lower disease prevalence for longer. | ||
| + | |||
| + | This means given an alternating sequence of $$R=R_1$$ and $$R=R_2$$ strategies, as prescribed by the "Only two values of $$R$$ are needed" argument, you would keeping swap adjacent periods until all of the $$R_1$$s come before all of the $$R_2$$s (assuming $$R_1<R_2$$ for the sake of argument). So you would end up with at most one change of strategy during the whole epidemic as you find yourself engaging in a single large period of $$R_1$$ followed by a large period of $$R_2$$. (Actually carrying this off would require being able to predict the timing of the end of the epidemic, which isn't easy in practice.) | ||
| + | |||
| + | The implied strategy is quite stark then: do all your lockdown to start with. In such a situation when your idealisation leads you to an extreme conclusion, it makes sense to check that the idealisation won't have broken down somewhere along the way. The kinds of things that could limit it are: (i) not being able to sustain the required lockdown for long enough: it's not completely true that lockdown+letup+lockdown is the same as lockdown+lockdown+letup because not everything can be put off indefinitely (otherwise this argument would imply that you could do lockdown for 10,000 years and then switch - i.e., it would obviously prove too much), (ii) the maths changes when the number of cases gets very low: it's not true that you can reduce cases until only $$10^{-100}$$ people are infected and then expect to be able to free everything up on the grounds that it would take a very long time for the virus to double its way back from such a low level. In reality you can extinguish the virus to zero incidence, as some countries have done, though then you have to consider the cost of protecting yourself from reinfection from the rest of the world. Or you could maintain the virus at a very low level that is consistent with the rate of reinfection from the rest of the world (which you would then obviously try to keep to a minimum). | ||
| + | |||
| + | At any rate, this argument would suggest that, at least before you hit limits like (i) and (ii) above (and possibly even then), it's better to go in hard first and never let the prevalence get high. | ||
= Conclusion = | = Conclusion = | ||
| − | * If further or stronger restrictions are imposed when $$R$$ is already less than $$1$$, then this may be a useful thing even though it seems masochistic, because it "builds up credit" in a way that | + | * If further or stronger restrictions are imposed when $$R$$ is already less than $$1$$ and disease levels are relatively low, then this may well be a useful thing even though it seems masochistic, because it "builds up credit" in a way that could be better overall. |
* If the policy alternates between strong and weak restrictions then this may be a good thing even if it seems as though the policy-makers can't make up their minds. | * If the policy alternates between strong and weak restrictions then this may be a good thing even if it seems as though the policy-makers can't make up their minds. | ||
* In the idealisation considered here a policy with three or more levels of restrictions is not useful (though it is still possible that such a multi-level policy makes sense due to this idealisation being too idealistic). | * In the idealisation considered here a policy with three or more levels of restrictions is not useful (though it is still possible that such a multi-level policy makes sense due to this idealisation being too idealistic). | ||
Latest revision as of 03:24, 15 January 2021
About
Description
The purpose of this is to take a broad look from a certain zoomed-out point of view at what kind of suppression strategies might be best. Here "suppression" is meant to mean that you intend to maintain infections in a low-level holding pattern until there is some favourable change in circumstances such as widespread immunity from a vaccine. I'm not trying to argue here against either infection-induced herd immunity or against zero-Covid/elimination strategies, just looking at what kinds of steady-state suppression strategies might work better than others. As of November 2020, most countries in the world are following a suppression strategy of some sort.
The reason I'm writing this is that when Covid-19 came on the scene in early 2020 I had a slight hunch that the best strategy of this form would be to alternate between strong and weak suppression. The discussion here is meant to explore the plausibility of this from a simplified point of view - it does not claim to prove it.
The abstraction here is that you just look at what values of the basic reproduction number, $$R$$, are best to aim at. This is an idealisation of the process of controlling a disease and ignores all sorts of things like how $$R$$ differs between regions and subcommunities, how to actually achieve a particular value of $$R$$, what the generation time is, how efficient it is to swap between different suppression states, what the effect of suppression on the distribution of infectivity time, to what extent the concept of $$R$$ actually makes sense, and so on, yet I would like to pursue it to see if there is any useful intuition to be obtained at this level. Is it better to keep $$R$$ hovering around 1, or is it better to mix strong suppression phases with relaxed phases? Should there be more than two sorts of such phases? Recently (as of November 2020) this has become topical again in the UK as we are trading off a relaxation over the Christmas period with some extra suppression before and after.
A suppression strategy means keeping the average growth rate of the disease equal to zero (or less). This is similar to keeping the multiplicative average $$R$$ at 1, though not quite the same (see below). For example if you alternate $$R=4$$ for 1 week and $$R=\frac12$$ for 2 weeks then the net effect over three weeks will be similar to an $$R$$ of $$4\times\frac12\times\frac12 = 1$$. This is because, to first approximation, $$R$$ is related to the growth rate $$\lambda$$ and the average time for an infected person to infect another (the mean generation time), $$T$$ by
\[R=e^{\lambda T}.\]
But because the time taken to infect someone is not a constant, a better formula is
\[R=r(\lambda)=\mathbb E[e^{-\lambda X}]^{-1},\]
where $$X$$ is the time to infection for each infectee, considered as a random variable. (Note, the above expectation uses a different probability space from that considered next.)
Consider the reproduction rate $$R$$ to be a random variable satisfying $$0<R\le R_0$$. Our goal (imagining ourselves to be the government) is to choose the best distribution for $$R$$. Here $$R_0$$ is the usual reproduction number in the absence of any distancing measures, which serves as an upper bound for $$R$$ under distancing. For example, $$\mathbb P(1<R<2)=1/4$$ would mean that we want be spending $$1/4$$ of the time with $$R$$ between $$1$$ and $$2$$. Let us suppose there is some utility function $$U(R)$$, increasing in $$R$$, that represents the benefit to society of maintaining a constant reproduction of $$R$$. For these purposes we'll assume that $$U()$$ is time-independent, though this isn't entirely realistic as seasonal factors, for example, will influence transmission rates and so how painful certain suppression measures are. Additive constants don't matter to $$U()$$, so it may be helpful to think of $$U(R)$$ negative and increasing up to $$U(R_0)=0$$. $$R=R_0$$ represents normal life in the absence of a pandemic, while negative $$U(R)$$ for $$R<R_0$$ represents the level of pain at implementing various levels of distancing/lockdown. Note that $$U(R)$$ is the utility when you fix the reproduction number at $$R$$; the possibility of varying this is what we're going to look at here and is represented by a mixture of different values of $$U()$$. For example, the strategy described in the preceding paragraph would have value $$\frac13(U(4)+2U(\frac12))$$. It seems reasonable that there is some version of the function $$U()$$ that represents reality to some extent, though of course it will be hard to agree upon any particular version of $$U()$$. We shall therefore try to see what we can deduce that doesn't depend on a precise $$U()$$, starting with observations that are more-or-less completely $$U()$$-independent, and ending with speculation that depends on a broad form of $$U()$$.
For these purposes it's more convenient to work with the growth rate $$\lambda$$, which we can consider as a random variable $$\Lambda$$ related to $$R$$ by $$R=r(\Lambda)$$. However, we shall also keep $$R$$ in the picture because it's probably more intuitive to people now as we've had experience of reproduction rates in the news. Using growth rate as the random variable, we can define $$V(\lambda)=U(r(\lambda))$$ and formulate the problem like this:
We wish to maximise
\[\mathbb E[V(\Lambda)]\]
subject to
\[\mathbb E[\Lambda]=0.\]
$$V()$$ is some increasing function and $$\Lambda\le\Lambda_0$$, where $$\Lambda_0$$ is defined by $$r(\Lambda_0)=R_0$$. This is meant to capture the time-independent aspect of the problem of medium/long term control of the virus: decide how long you want to spend at different lockdown levels, and factor out "implementation details" of how/when to switch from one level to another. Obviously in reality such "details" are very important and may in practice be a sticking point but still I think it's interesting to consider what kinds of distributions are likely to make sense.
Note that we don't consider the possibility of $$\mathbb E[\Lambda]<0$$ even though this would also result in disease suppression, because $$V()$$ is increasing so if $$-\infty<\mathbb E[\Lambda]<0$$ we may as well increase $$\Lambda$$ a bit to improve $$\mathbb E[V(\Lambda)]$$ and maintain suppression. And $$\mathbb E[\Lambda]=-\infty$$ is a zero-Covid strategy (leading to extinction of the disease) which we are not considering here, so in particular we must have $$\mathbb P(\Lambda=-\infty)=\mathbb P(R=0)=0$$.
Only two values of $$R$$ are needed
Equivalently, only two values of $$\Lambda$$ are needed. Suppose that $$\Lambda$$ only takes finitely many values (which isn't a very onerous restriction): $$\mathbb P(\Lambda=\lambda_i)=p_i$$ for $$i=1,\ldots, n$$, where $$p_i>0$$ and $$0<r_1<\ldots<r_n$$. If $$n\ge3$$ then we can consider the effect of adjusting the probabilities $$(p_1, p_2, p_3)$$ by a multiple of $$(\Delta p_1, \Delta p_2, \Delta p_3)=(\lambda_2-\lambda_3, \lambda_3-\lambda_1, \lambda_1-\lambda_2)$$ since that preserves $$\sum_i p_i$$ and $$\sum_i p_i\lambda_i$$. If $$\Delta V = V(\lambda_1)\Delta p_1+V(\lambda_2)\Delta p_2+V(\lambda_3)\Delta p_3\ge0$$ then we can improve the overall value by adding on a positive multiple of $$(\Delta p_1, \Delta p_2, \Delta p_3)$$, while if $$\Delta V\le0$$ we can use a negative multiple. Either way we can change $$p_1, p_2, p_3$$ until one of them becomes $$0$$. This demonstrates that we only need to consider $$n=1$$ or $$n=2$$.
This is slightly interesting. Based only on fairly mild assumptions, it means you only want to be aiming for at most two states: relatively locked down or relatively relaxed (or with $$n=1$$, aim for just one state), and not using anything in between. Of course this is only absolutely true within the idealisation we have used and doesn't automatically invalidate the multi-tiered approach which many countries have adopted. In the real world you don't know exactly what $$R$$ you will get from a particular set of measures, so it may be useful to have a responsive set of measures that are able to nudge $$R$$ down or up a bit.
Should we use 1 or 2 values of $$R$$?
I think this is the most interesting question here. Do you (as the government) go for $$n=1$$ which means a steady state of continuous medium-level suppression trying to fix $$R$$ at $$1$$, or do you go for $$n=2$$ which means deliberately bouncing between strong and weak suppression? Of course we can't properly answer this question here because it would require a large amount of real-world data that we don't have, but we can at least see what we can say about this objectively to see if that gives any useful feeling for the question. In the next section we'll look at some real-world data and I'll state my hunch (which is that $$n=2$$).
In the real world the two strategies could blur together somewhat since tracking $$R=1$$ ($$\Lambda=0$$) would involve some trial and error as you nudge $$R$$ up or down a bit according to whether infections are seen to be under control or getting too high, but there would still be a distinction. I think this $$n=1$$ strategy is the one that's most obvious to people, though it isn't necessarily the best. $$n=2$$ could seem counterintuitive because if the disease prevalence is relatively low, and if the current value of $$R$$ is $$1$$ so things are nicely under control, you are asking people to increase distancing measures to get $$R$$ down even further, and they will surely ask you what the point is of doing that. On the face of it, it will seem as though there is no benefit in enduring the pain of $$R=0.8$$ when infections have already stabilised at a manageable level, but the point is that further reducing disease prevalence is a kind of investment, and can be redeemed later when you get to indulge in a period of (for example) $$R=1.5$$.
(Somewhat speculative, but I have got the impression from the way we've opened up since April, and from the way that the progressive relaxation of measures was couched in terms of how much we can afford to do while still keeping the virus under control, that we might have fallen into the trap of thinking that it's necessarily optimal to open up as much as we can while keeping $$R\le1$$. That is, we might be following the $$n=1$$ strategy by default.)
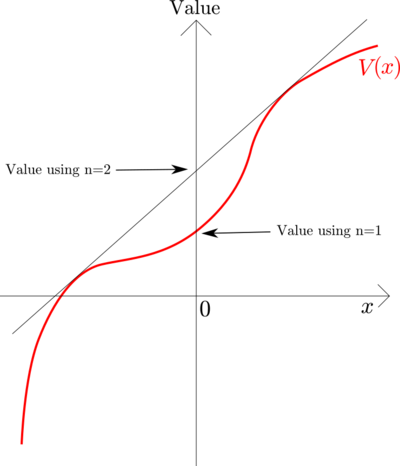
Let's say that $$\Lambda$$ takes the two values $$a$$ and $$b$$, where $$-\infty<a<0<b\le\Lambda_0$$. $$n=1$$ is a limiting case of this where $$a=b=0$$. $$\mathbb E[\Lambda]=0$$ means that $$\mathbb P(\Lambda=a)=b/(b-a)$$ and $$\mathbb P(\Lambda=b)=-a/(b-a)$$. The objective then is to maximise \[\mathbb E[V(\Lambda)]=\frac{bV(a)-aV(b)}{b-a}\] over \[-\infty<a<0<b\le\Lambda_0.\]
Geometrically, we join two points on the graph of $$V(x)$$ on either side of $$x=0$$, and see how high this chord is at $$x=0$$. $$n=1$$ would mean just using $$V(0)$$.
The condition for $$n=1$$ doing better than $$n=2$$ is a concavity condition on $$V()$$ at $$0$$: is the graph of $$V()$$ below its tangent at $$0$$ or not? This is ultimately an empirical question that would need a lot of work to determine.
For what it's worth, my guess is that $$V()$$ could look something like the above picture. A somewhat handwavy reasoning follows. At one end ($$\lambda\ll0$$) there are contacts you can't do without: parents looking after children, getting food, hospitals looking after sick etc., which means $$V(\lambda)$$ probably drops off sharply as $$\lambda\to-\infty$$. At the other end ($$\lambda\gg0$$) there are probably some easy measures to take that have a decent effect on disease growth (hand hygiene, masks, avoiding some unnecessary close contact etc.) but which don't come at a large cost, which means $$V(\lambda)$$ is relatively flat there. But in the middle, you might expect $$U(R)$$ to be roughly linear in $$R$$ because there are lots of useful-but-not-essential things, and the benefit you get from them is roughly the amount you can do them. For plausible infectivity distributions, $$V()$$ tends to be more convex than $$U()$$ (see next section), so that $$U()$$ being locally linear near 1 would make $$V()$$ locally convex near 0.
(Incidentally, if $$V(\lambda)$$ is bounded below, or even if $$V(\lambda)/\lambda\to0$$ as $$\lambda\to-\infty$$, then the optimal strategy will be approached by mixing a very small chance of an arbitrarily negative $$\lambda$$ with a large chance of $$\Lambda=\Lambda_0$$ ($$b=\Lambda_0$$, $$a\to-\infty$$), getting an expectation arbitrarily close to $$V(\Lambda_0)=U(R_0)$$. But I think this situation isn't realistic because some contacts between people are essential.)
Real world data
We've seen theoretical arguments about the plausible form of $$U()$$ or $$V()$$. How does the real world inform us? In practice it's going to be hard to extract a great deal of information without a great deal of work, so I'm not going to attempt that here. Instead we can just take a look at kind of trade-offs we might expect.
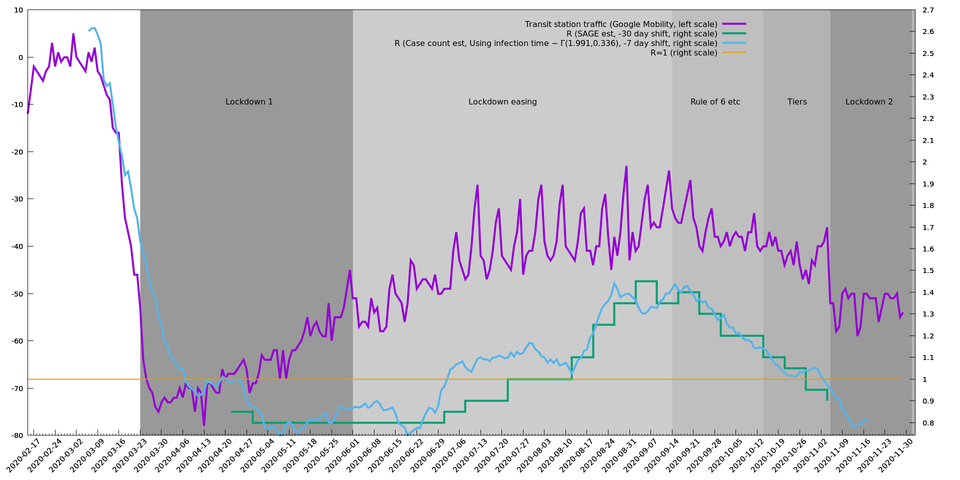
In this graph, the green line is the Government Office for Science and SAGE estimate of $$R$$, with weekly updates starting 15 May 2020. The documentation suggests it might lag by 21 days, but it looks a bit like 21 may not be enough and you have to bring the graph forward by around 30 days to match the blue line from August 2020. (Maybe the 21 days is only the lag from antigen test to publication and doesn't take into account the time between infection and test?)
The blue line is the ratio of smoothed case counts (from the UK Covid-19 dashboard) at day $$d$$ and $$d+14$$, where $$d$$ is the x-coordinate on this graph. This effectively brings it forward by 7 days which should roughly account for incubation+testing+reporting delays. This is naturally in units of growth ($$\lambda$$) rather than $$R$$, but I'm making the y-axis $$R$$ rather than growth rate because I think people are more used to $$R$$. The conversion formula used here is $$R=(1+\lambda/\beta)^\alpha$$, where $$\alpha=1.99$$ and $$\beta=0.336$$. This is what $$r(\lambda)$$ (see above) works out as if the mean generation time, $$X$$, is distributed as $$\Gamma(\alpha,\beta)$$ (*), using the (shape,rate) notation. These values of $$\alpha$$, $$\beta$$ were fitted to the SAGE estimates (green line), which is possible because they publish both $$R$$ and growth rate. So even if this conversion formula isn't quite right, it should therefore make the blue and green lines comparable. In any case when $$R$$ is close to $$1$$, $$R-1$$ is going to be close to proportional to the growth rate.
The blue line probably overestimates $$R$$ because testing has been steadily increasing, so we're likely to be finding a greater proportion of cases as time goes on. In particular in April there was a sudden explosion in available tests, which may account for the blue line being at $$R~=1$$ then when the true value was probably more like $$0.8$$. At a guess, later blue line entries are closer to their true values.
The REACT 1 survey provides another estimate of $$R$$, but is not shown here. This tends to give slightly more moderate values of $$R$$, meaning closer to $$1$$. (Aside: As far as I can see they are using a slightly dodgy estimate of the mean generation time distribution. On page 4 of this paper they state they use $$X\sim\Gamma(2.29,2.29/6.29)$$ derived from Bi et al, but the latter is an estimate of the serial interval distribution not the mean generation time, so will have the right mean but a larger (possibly considerably larger) variance. I also think it may be slightly dubious to use an estimate from Jan-Feb 2020 in Shenzhen and apply it to Western countries with different cultures, age demographics and suppression measures. It may be OK as a starting point estimate, but I'm not sure that they revisit it. One might expect that suppression measures will tend to reduce the mean and variance of $$X$$ as more symptomatic than asymptomatic people isolate themselves.)
The purple line is there for reference as an external measure of how locked down the country is over time. It uses the "transit stations percent change from baseline" from the Google Mobility Data source, which we might expect to be a proxy for how much people are going to work, going out to meet, etc., though it obviously doesn't tell the whole story. [Aside, some features: we can see that this measure of mobility significantly reduced in the two weeks before the first lockdown on 23 March as people were either following the pre-lockdown restrictions or were taking matters into their own hands. And in the month or so before the tiers system was introduced on 14 October there was a fall in mobility, perhaps because the "mood music" had shifted from people feeling the disease was on its way out to realising that it wasn't going away just yet. And before the second lockdown, at around 2-4 November, it looks like there was some kind of blow-out as people partied away before the new restrictions on 5 November - this spike can be seen on other data sources.]
It looks like for an $$R=1$$ strategy we'd have to stick to a level of restrictions roughly equivalent to those in July. The blue line would suggest the beginning of July and the green line, the end of July, so it's hard to tell exactly what this entails as there was quite a lot of easing up during July, for example with pubs and hairdressers closed at the start of the month and open at the end. In either case, this is a snapshot of the restrictions in place on 31 July 2020.
For an example of a strong/weak policy, one could combine the $$R=1.4$$ state in mid-September at the height of the loosening with $$R=0.8$$ of May (or possibly November during "Lockdown 2"). This would have to be taken in the ratio of something like 1:2, for example one month of $$R=1.4$$ followed by two of $$R=0.8$$. The restrictions in place on 20 May 2020 can be found here while those in place on 13 September 2020 can be found here.
However, if the strongest lockdown we can manage only has $$R$$ as low as $$0.7-0.8$$, which is what we've managed hitherto, then intuition suggests that the benefits of a two-level strategy are probably not that great. Roughly speaking, if you do something like mix $$R=0.8$$ with $$R=1.25$$ in equal proportions then the average $$R$$ value (a proxy for the overall benefit) is only $$1.025$$. You'd get a more useful gain if you could mix something like $$R=0.5$$ with $$R=2$$ for an average $$R$$ of $$1.25$$ (we should really be working with growth not $$R$$, but this is just a rough thought), though I don't know if an $$R=0.5$$ regime is practically possible.
(*) It's common to use the Gamma distribution here because it's a very convenient two-parameter family of non-negative distributions, not because there is a particular reason to expect the distribution to have this precise form. (And there isn't usually enough data to fit more than two parameters.) If $$X\sim\Gamma(\alpha,\beta)$$ then $$V(\lambda)=U(\theta^\alpha)$$, where $$\theta=1+(\alpha/\beta)\lambda$$, and $$V''(\lambda)=(\alpha/\beta)^2\theta^{2\alpha-2}U''(\theta^\alpha)+(\alpha(\alpha-1)/\beta^2)\theta^{\alpha-2}U'(\theta^\alpha)$$, so provided $$\alpha>1$$, which is what everyone thinks, then $$V()$$ is "more convex" than $$U()$$ because $$V''$$ has an extra term that is always positive.
An alternative (and simpler) argument
Given a period of $$R=R_1$$ for time $$T_1$$ followed by a period of $$R=R_2$$ for time $$T_2$$, then swapping these two periods around (doing $$R=R_2$$ for time $$T_2$$ first) doesn't change anything before or after the two periods. At least, this is true in the idealisation we've been considering here where the policy in each period multiplies the disease prevalence by a factor independent of the incoming prevalence: granted this, it doesn't matter which order we multiply these two factors. But during the two periods, it's better to take the smaller $$R$$ first since you'd then enjoy lower disease prevalence for longer.
This means given an alternating sequence of $$R=R_1$$ and $$R=R_2$$ strategies, as prescribed by the "Only two values of $$R$$ are needed" argument, you would keeping swap adjacent periods until all of the $$R_1$$s come before all of the $$R_2$$s (assuming $$R_1<R_2$$ for the sake of argument). So you would end up with at most one change of strategy during the whole epidemic as you find yourself engaging in a single large period of $$R_1$$ followed by a large period of $$R_2$$. (Actually carrying this off would require being able to predict the timing of the end of the epidemic, which isn't easy in practice.)
The implied strategy is quite stark then: do all your lockdown to start with. In such a situation when your idealisation leads you to an extreme conclusion, it makes sense to check that the idealisation won't have broken down somewhere along the way. The kinds of things that could limit it are: (i) not being able to sustain the required lockdown for long enough: it's not completely true that lockdown+letup+lockdown is the same as lockdown+lockdown+letup because not everything can be put off indefinitely (otherwise this argument would imply that you could do lockdown for 10,000 years and then switch - i.e., it would obviously prove too much), (ii) the maths changes when the number of cases gets very low: it's not true that you can reduce cases until only $$10^{-100}$$ people are infected and then expect to be able to free everything up on the grounds that it would take a very long time for the virus to double its way back from such a low level. In reality you can extinguish the virus to zero incidence, as some countries have done, though then you have to consider the cost of protecting yourself from reinfection from the rest of the world. Or you could maintain the virus at a very low level that is consistent with the rate of reinfection from the rest of the world (which you would then obviously try to keep to a minimum).
At any rate, this argument would suggest that, at least before you hit limits like (i) and (ii) above (and possibly even then), it's better to go in hard first and never let the prevalence get high.
Conclusion
- If further or stronger restrictions are imposed when $$R$$ is already less than $$1$$ and disease levels are relatively low, then this may well be a useful thing even though it seems masochistic, because it "builds up credit" in a way that could be better overall.
- If the policy alternates between strong and weak restrictions then this may be a good thing even if it seems as though the policy-makers can't make up their minds.
- In the idealisation considered here a policy with three or more levels of restrictions is not useful (though it is still possible that such a multi-level policy makes sense due to this idealisation being too idealistic).